无常损失在理论上具有可逆性——当代币价格完全恢复至初始存入比例时,无常损失可以消失;但在实际操作中,恢复效果受价格波动幅度、频率、手续费收益等多重因素影响,并非绝对可逆。以下从机制原理、实际限制、历史案例到应对策略展开深度分析。
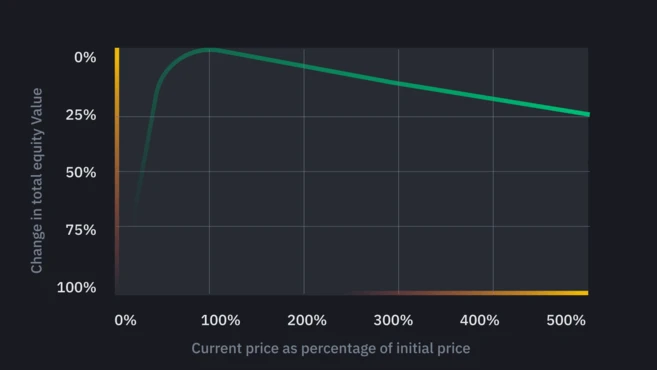
一、核心定义:为何会产生无常损失?
无常损失是流动性提供者(LP)在AMM(自动化做市商)机制下,因代币价格偏离初始存入比例而产生的资产价值损失。其本质源于AMM的恒定乘积公式 ( x \cdot y = k )(x和y分别代表两种代币数量,k为常数):当市场价格变化时,AMM会自动调整代币数量以维持k值,导致LP持有的资产组合价值低于“单纯持有代币”的价值。
举例:若LP存入1 ETH(价格1000 DAI)和1000 DAI,初始比例为1:1000。当ETH价格涨至2000 DAI时,AMM会自动减少ETH数量、增加DAI数量以维持k值。此时LP持有的ETH减少、DAI增多,但按新价格计算,资产组合价值(约1414 DAI)低于“持有1 ETH+1000 DAI”的价值(2000+1000=3000 DAI),差额即为无常损失。
二、理论可逆性:价格回归原点,损失为何会消失?
根据AMM恒定乘积公式,当代币价格完全恢复至初始比例时,LP的资产组合价值将与初始值一致,无常损失理论上归零。这是因为价格回归意味着x和y的乘积k虽经波动但最终回到初始状态,资产数量比例重新匹配初始存入时的市场价格。
数学验证:假设初始状态为( x_0 \cdot y_0 = k ),价格波动后变为( x_1 \cdot y_1 = k ),当价格回归,( x_2 \cdot y_2 = k )且( x_2/y_2 = x_0/y_0 ),此时( x_2 = x_0 )、( y_2 = y_0 ),资产价值完全恢复。
三、实际限制:价格回升≠损失必然恢复
尽管理论上可逆,但实际操作中,无常损失的恢复受以下因素制约:
1. 波动幅度与频率:多次波动可能产生累积损失
若价格经历“上涨-下跌-再上涨”的多次波动,即使最终回归原点,中间过程的套利行为可能导致LP资产组合的“被动调仓”,形成累积损失。例如,代币价格先涨50%再跌33%(理论上回归原价),但两次波动中AMM的自动平衡会使LP持有的高价代币比例持续降低,最终资产总量可能低于初始值。
2. 手续费收益:部分抵消但非“万能解药”
LP通过交易手续费获得收益,可能抵消部分无常损失。但2025年DeFi协议手续费模型趋于复杂(如动态费率、协议代币奖励叠加),手续费能否覆盖损失取决于:
- 交易频率:高交易量池(如Uniswap V3的ETH-USDC池)手续费累积更快;
- 波动周期:短期剧烈波动可能导致手续费尚未累积,损失已形成;
- 资金成本:若LP资金有借贷成本(如质押借贷获取流动性),手续费需先覆盖利息才能真正“补偿”。
3. 滑点与市场深度:小资金池更脆弱
小资金池因市场深度不足,价格波动时易被套利者利用,导致滑点扩大和资产损耗。例如,某小盘代币对价格短暂偏离时,套利者会迅速交易使价格回归,但LP资产已因高频套利产生额外损失,即使价格最终恢复,实际价值也可能缩水。
四、历史案例:价格回升后,损失真的消失了吗?
1. ETH/DAI池(2023年):损失归零但资金成本未覆盖
2023年ETH价格因监管消息暴跌后反弹,某LP在价格完全恢复后观察到无常损失归零,但手续费收益仅覆盖约30%的资金成本。原因是价格波动期间交易频率下降,手续费累积不足,且LP为获取流动性使用了借贷资金,利息成本侵蚀了最终收益。
2. BCH价格短暂波动(2025年6月):损失消失但持仓比例被动调整
2025年6月,BCH因市场情绪导致价格在24小时内先跌15%再涨15%(理论回归原价)。LP发现无常损失随价格回落消失,但持仓中BCH数量减少、USDT数量增加——这是因为价格下跌时AMM自动买入BCH,上涨时卖出BCH,最终持仓比例与初始状态不同,若后续价格再次波动,损失风险可能变化。
五、策略建议:如何应对无常损失的“可逆性陷阱”?
1. 长期持有者:以时间换空间
若坚定看好代币长期价值(如BTC、ETH),可容忍短期无常损失。历史数据显示,长期价格回归周期中(如1-2年),手续费收益叠加价格回升,LP综合收益可能超过单纯持有(需注意协议风险,如智能合约漏洞)。
2. 风险规避者:选择低波动场景
- 稳定币对:如USDC/USDT池,价格波动极小(通常<1%),无常损失可忽略;
- 新型AMM模型:Curve的StableSwap针对稳定币优化,采用分段函数降低波动敏感性;Balancer的权重池允许自定义代币比例(如80%ETH+20%稳定币),减少单边波动影响。
3. 动态调整:设定波动阈值
监控价格偏离初始比例的阈值(如±10%),触发时补充流动性或撤出部分资金。例如,当ETH价格上涨10%,可追加ETH以维持初始比例,降低后续波动中的损失风险(需权衡gas成本与潜在收益)。
六、总结:理论可逆,实操需权衡
无常损失的“可逆性”本质是价格回归原点时的数学结果,但现实中受波动频率、手续费模型、资金池深度等多重因素影响。对LP而言,关键在于:
- 评估价格回归概率:高波动性代币(如MEME币)价格回归难度大,无常损失可能长期存在;
- 计算手续费平衡点:若手续费年化收益>预期波动损失,即使价格不回归,仍可通过手续费盈利;
- 匹配风险偏好:稳定币对适合保守者,高波动对适合风险承受能力强的长期持有者。
最终,无常损失的“可逆性”不是绝对承诺,而是一个需要结合市场环境、策略选择的动态平衡过程。